Pontos no Plano Cartesiano

A Geometria Analítica estuda as propriedades das figuras geométricas estabelecendo uma relação entre a Geometria Plana e a Álgebra. Toda figura geométrica pode ser analisada como um conjunto de pontos e para traduzirmos em linguagem algébrica as propriedades destas figuras geométricas associamos esses pontos a números.
Podemos marcar um ponto em uma régua, por exemplo, vamos marcar o ponto onde fica o 3 em nossa régua:

Desta forma estamos associando o ponto A ao número 3. Podemos marcar assim todos os pontos existentes nessa régua. Mas esta nossa régua é limitada, como faríamos para representar o ponto associado ao número 1023? Ou ao número - 57, ou ainda ao número 0,0000356? Ou seja, como marcaríamos os pontos que não pertencem a esta régua? Para isso estabelecemos um sistema de coordenadas sobre uma reta onde associamos cada ponto desta reta a um número real, como na figura abaixo:

O ponto C está associado ao número real 1. Podemos afirmar então que a coordenada do ponto C é o número real 1.
Na figura abaixo encontramos outra limitação da nossa régua:

Se dissermos que existe um ponto associado ao número 3 não será suficiente para determinar de qual ponto estamos falando A ou B. Pois A está mais distante da régua que B. Para determinarmos a localização de A e B usaremos uma outra régua mas desta vez na vertical.

Agora sim podemos determinar a localização dos pontos A e B. A está associado ao número 3 na régua horizontal e ao número 6 na régua vertical. B também está associado ao número 3 na régua horizontal mas na régua vertical está associado ao número real 4. Chamamos estas duas coordenadas de cada ponto de par ordenado.
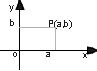
Com as réguas acima ficamos limitados aos números positivos menores que 15. Para determinarmos a localização de qualquer ponto precisaríamos de duas réguas infinitas. Representamos a correspondência entre os pontos do plano e o conjunto de pares ordenados de números reais por duas retas infinitas e perpendiculares denominadas eixos ortogonais que formam o sistema cartesiano ortogonal. O eixo horizontal é chamado de eixo x ou eixo das abscissas e o eixo vertical é chamado de eixo y ou eixo das ordenadas. Na figura abaixo podemos observar que o ponto C está associado ao par ordenado (257,143). Considerando o ponto D(-200,-100) dizemos que o número -200 é a coordenada x ou a abscissa do ponto D e o número -100 é a coordenada y ou a a ordenada do ponto D.

Os eixos coordenados dividem o plano cartesiano em 4 regiões chamadas quadrantes como na figura abaixo.

Lembre-se que os eixos coordenados são infinitos e portanto as regiões definidas por eles também são, isto é:
1º quadrante: região onde os pares ordenados associados aos pontos tem como abscissa números reais maiores que 0 e como ordenadas números reais maiores que zero, ou seja, x > 0 e y > 0.
2º quadrante: região onde os pares ordenados associados aos pontos tem como abscissa números reais menores que 0 e como ordenadas números reais maiores que zero, ou seja, x < 0 e y > 0.
3º quadrante: região onde os pares ordenados associados aos pontos tem como abscissa números reais menores que 0 e como ordenadas números reais menores que zero, ou seja, x < 0 e y < 0.
4º quadrante: região onde os pares ordenados associados aos pontos tem como abscissa números reais maiores que 0 e como ordenadas números reais menores que zero, ou seja, x > 0 e y < 0.

O ponto de intersecção dos eixos x e y, O(0,0), é chamado de origem e pertence aos dois eixos. Os pontos situados sobre os eixos coordenados por convenção não pertencem a nenhum quadrante.

Marcar pontos no software Geogebra é muito fácil, acompanhe a atividade 1:

atividade 1

Tutorial do Geogebra

Atividade 2

Álgebra

Álgebra

X? Y? Entenda os cálculos com letras

Carlos Alberto Campagner*

Para representar os problemas da vida real em linguagem matemática, muitas vezes utilizamos letras que substituem incógnitas (os valores que você não conhece, e quer descobrir). É aí que entram os famosos x, y, etc. O ramo da matemática que utiliza símbolos (normalmente letras do nosso alfabeto latino e do grego) para a resolução de problemas é chamado álgebra.

As equações são a aplicação mais conhecida dessa área da matemática.

Por exemplo, a área de um retângulo de base b e altura c é dada pela fórmula:

A = b . c

Esse monte de letra nada mais é que a representação de "fatos da vida real" por meio de números: a representa a área, b e c representam os lados do retângulo.

Essa fórmula vale para qualquer retângulo cuja área se deseja calcular.

Letras substituem valores iguais

Como você resolveria o seguinte cálculo?

<>

Imagine que x represente um objeto, por exemplo, uma maçã. Então você faria:

"3 maçãs mais 7 maçãs"

Logicamente o resultado é "10 maçãs". Então:

<>

O procedimento, como você viu, é simples: para somar números que acompanham incógnitas, basta somá-los, normalmente (desde que as incógnitas sejam iguais).

Agora suponha que x valha 17 maçãs. O resultado de nossa operação seria 170.

Problemas resolvidos pela álgebra

Vamos descobrir quanto medem os lados de um retângulo em que um lado é o dobro do outro e cujo perímetro é igual a 60.

<>

Para começar, é necessário saber o que é perímetro - é a soma de todos os lados de uma figura geométrica.

Como um lado foi chamado de x, o outro - que é o dobro - será 2x.

Nesse caso, o perímetro pode ser escrito como a soma dos 4 lados:

<>

Logo:

<>

Como o perímetro deve ser igual a 60, o único número que multiplicado por 6 resulta 60 é o número 10, logo:

<>

Geometria analítica

A geometria analítica, também chamada geometria de coordenadas e que antigamente recebia o nome de geometria cartesiana, é o estudo da geometria através dos princípios da álgebra. Em geral, é usado o sistema de coordenadas cartesianas para manipular equações para planos, retas, curvas e círculos, geralmente em duas dimensões, mas por vezes também em três ou mais dimensões. Alguns pensam que a introdução da geometria analítica constituiu o início da matemática moderna. Os estudos iniciais da Geometria Analítica se deram no século XVII , e devem-se ao filósofo e matemático francês René Descartes (1596 - 1650), inventor das coordenadas cartesianas (assim chamadas em sua homenagem), que permitiram a representação numérica de propriedades geométricas.

Por aquilo que dela é ensinado nos livros escolares, pode-se explicar a geometria analítica de uma forma mais simples: a disciplina procura definir formas geométricas de modo numérico e extrair informação numérica dessa representação. O resultado numérico também pode, no entanto, ser um vector ou uma forma.

René Descartes criou as fundações para os métodos da geometria analítica em 1637 no apêndice intitulado Geometria do seu Discurso do Método. Este livro e os seus princípios filosóficos criaram as fundações para o cálculo, que foi mais tarde introduzido independentemente por Isaac Newton e Gottfried Wilhelm Leibniz.

Os temas importantes de geometria analítica incluem:

• Espaço vectorial
• Definição do plano
• Problemas de distância
• O produto escalar para obter o ângulo entre dois vectores
• O produto vectorial para obter um vector perpendicular a dois vectores conhecidos (e também o seu volume espacial)
• Problemas de intersecção

Alguns destes problemas envolvem álgebra linear.

A geometria analítica, no contexto da geometria algébrica, é também o nome da teoria das variedades complexas e dos mais gerais espaços analíticos. Está ligada à geometria algébrica, especialmente pelo trabalho de Serre.

Introdução a Geometria Analítica

1 - Introdução
A Geometria Analítica é uma parte da Matemática , que através de processos particulares , estabelece as relações existentes entre a Álgebra e a Geometria. Desse modo , uma reta , uma circunferência ou uma figura podem ter suas propriedades estudadas através de métodos algébricos .
Os estudos iniciais da Geometria Analítica se deram no século XVII , e devem-se ao filósofo e matemático francês René Descartes (1596 - 1650), inventor das coordenadas cartesianas (assim chamadas em sua homenagem), que permitiram a representação numérica de propriedades geométricas. No seu livro Discurso sobre o Método, escrito em 1637, aparece a célebre frase em latim "Cogito ergo sum" , ou seja: "Penso, logo existo".
1.1 - Coordenadas cartesianas na reta
Seja a reta r na Fig. abaixo e sobre ela tomemos um ponto O chamado origem.
Adotemos uma unidade de medida e suponhamos que os comprimentos medidos a partir de O, sejam positivos à direita e negativos à esquerda.

O comprimento do segmento OA é igual a 1 u.c (u.c = unidade de comprimento). É fácil concluir que existe uma correspondência um a um (correspondência biunívoca) entre o conjunto dos pontos da reta e o conjunto R dos números reais. Os números são chamados abscissas dos pontos. Assim, a abscissa do ponto A’ é -1, a abscissa da origem O é 0, a abscissa do ponto A
é 1, etc.
A reta r é chamada eixo das abscissas.

1.2 - Coordenadas cartesianas no plano
Com o modo simples de se representar números numa reta, visto acima, podemos estender a idéia para o plano, basta que para isto consideremos duas retas perpendiculares que se interceptem num ponto O, que será a origem do sistema. Veja a Fig. a seguir:

Dizemos que a é a abscissa do ponto P e b é a ordenada do ponto P.
O eixo OX é denominado eixo das abscissas e o eixo OY é denominado eixo das ordenadas.
O ponto O(0,0) é a origem do sistema de coordenadas cartesianas.
Os sinais algébricos de a e b definem regiões do plano denominadas QUADRANTES.
No 1º quadrante, a e b são positivos, no 2º quadrante, a é negativo e b positivo, no 3º quadrante, ambos são negativos e finalmente no 4º quadrante a é positivo e b negativo.

Observe que todos os pontos do eixo OX tem ordenada nula e todos os pontos do eixo OY tem abscissa nula. Assim, dizemos que a equação do eixo OX é y = 0 e a equação do eixo OY é
x = 0.
Os pontos do plano onde a = b, definem uma reta denominada bissetriz do 1º quadrante, cuja equação evidentemente é y = x.
Já os pontos do plano onde a = -b (ou b = - a), ou seja, de coordenadas simétricas, definem uma reta denominada bissetriz do 2º quadrante, cuja equação evidentemente é y = - x.
Os eixos OX e OY são denominados eixos coordenados.

EXERCICIO DE FIXAÇÃO

1) Se o ponto P(2m-8 , m) pertence ao eixo dos y , então :
a) m é um número primo
b) m é primo e par
c) m é um quadrado perfeito
d) m = 0
e) m < 4

2) Se o ponto P(r - 12 , 4r - 6) pertença à primeira bissetriz , então podemos afirmar que :
a) r é um número natural
b) r = - 3
c) r é raiz da equação x³ - x² + x + 14 = 0
d) r é um número inteiro menor do que - 3 .
e) não existe r nestas condições .

3) Se o ponto P(k , -2) satisfaz à relação x + 2y - 10 = 0 , então o valor de k ² é :
a) 200
b) 196
c) 144
d) 36
e) 0

2 - Fórmula da distância entre dois pontos do plano cartesiano

Dados dois pontos do plano A(Xa,Ya) e B(Xb,Yb) , deduz-se facilmente usando o teorema de Pitágoras a seguinte fórmula da distancia entre os pontos A e B:

Esta fórmula também pode ser escrita como: d²_AB = (X_b - X_a)² + (Y_b - Y_a)² , obtida da anterior, elevando-se ao quadrado (quadrando-se) ambos os membros.

EXERCÍCIO DE FIXAÇÃO

O ponto A pertence ao semi-eixo positivo das ordenadas ; dados os pontos B(2 , 3) e C(-4 ,1) , sabe-se que do ponto A se vê o segmento BC sob um ângulo reto . Nestas condições podemos afirmar que o ponto A é :
a) (3,0)
b) (0, -1)
c) (0,4)
d) (0,5)
e) (0, 3)

3 - Ponto médio de um segmento

Dado o segmento de reta AB , o ponto médio de AB é o ponto M Î AB tal que AM = BM .
Nestas condições, dados os pontos A(x₁ , y₁) e B(x₂ , y₂) , as coordenadas do ponto médio
M(x_m , y_m) serão dadas por:

EXERCÍCIO DE FIXAÇÃO

Sendo W o comprimento da mediana relativa ao lado BC do triângulo ABC onde A(0,0), B(4,6) e C(2,4) , então W² é igual a:
a) 25
b) 32
c) 34
d) 44
e) 16

LEIA COM ATENÇÃO O ASSUNTO Á SEGUIR; POIS IREMOS VER NAS PROXIMAS AULAS. QUALQUER DÚVIDA PODE SER TIRADA NO MSN OU NO FACEBOK:silvia-nery@live.com NOS HORÁRIOS TERÇAS DE 14:00 ás 16:00 3ºRO1 - RO2 APARTI DAS 16:30 ÁS 18:30

4 - Baricentro de um triângulo
Sabemos da Geometria plana , que o baricentro de um triângulo ABC é o ponto de encontro das 3 medianas . Sendo G o baricentro , temos que AG = 2 . GM onde M é o ponto médio do lado oposto ao vértice A (AM é uma das 3 medianas do triângulo).
Nestas condições , as coordenadas do baricentro G(x_g , y_g) do triângulo ABC onde A(x_a , y_a) , B(x_b , y_b) e C(x_c , y_c) é dado por :


Conclui-se pois que as coordenadas do baricentro do triângulo ABC, são iguais às médias aritméticas das coordenadas dos pontos A , B e C.
Assim, por exemplo, o baricentro (também conhecido como centro de gravidade) do triângulo ABC onde A(3,5) , B(4, -1) e C(11, 8) será o ponto G(6, 4). Verifique com o uso direto das fórmulas.

Exercício resolvido

Conhecendo-se o baricentro B(3,5), do triângulo XYZ onde X(2,5) , Y(-4,6) , qual o comprimento do segmento BZ?
Solução:Seja o ponto Z(a,b). Temos, pela fórmula do baricentro:
3 = (2 - 4 + a) / 3 e 5 = (5 + 6 + b) / 3
Daí, vem que a = 11 e b = 4. O ponto Z será portanto Z(11, 4).
Usando a fórmula da distância entre dois pontos, lembrando que B(3,5) e Z(11,4),
encontraremos BZ = 65^1/2 u.c. (u.c. = unidades de comprimento).
Agora resolva este:
Os pontos A(m, 7), B(0, n) e C(3, 1) são os vértices de um triângulo cujo baricentro é o ponto
G(6, 11). Calcule o valor de m² + n².
Resposta: 850